---

ASSIGNMENT #5: Von Koch Snowflake

---

Score: 10 points

---

The Von Koch Snowflake is a nice example how to use recursion to create interesting graphics. Besides that it and its relatives are the topic of serious research in math, but for now we are just interested in recursion and beauty.

Results first: Here's your task. Please write a recursive program that creates this output:

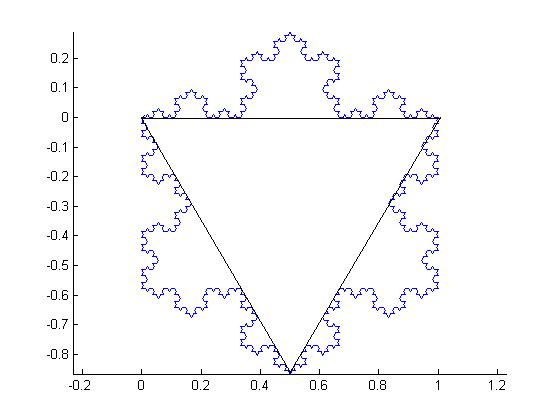
(remark: please visualize the snowflake only, not the triangle in the middle, and not the coordinate axes shown in the figure above. I programmed the curve in matlab, that's why the axes are shown).

The snowflake you see developed from the triangle in the center by recursively applying a simple rule to each of the triangles sides. The Rule, which i deliberately state iteratively here:
- cut the side (of length l) into 3 equal parts (of length l/3)
- replace the center part with 2 sides of length l/3, such that it forms a spike

- repeat the process for each of the 4 sides, until the length of each side is smaller than a given value.

The following figure visualizes this construction rule.

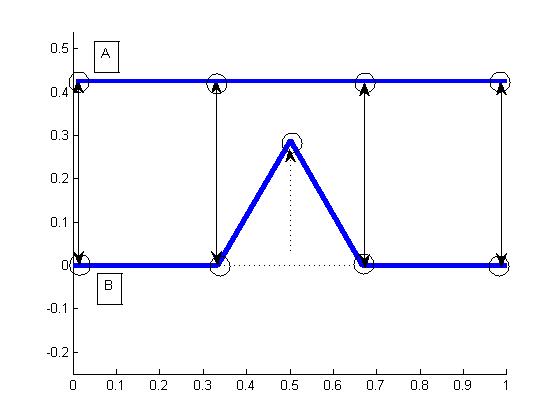
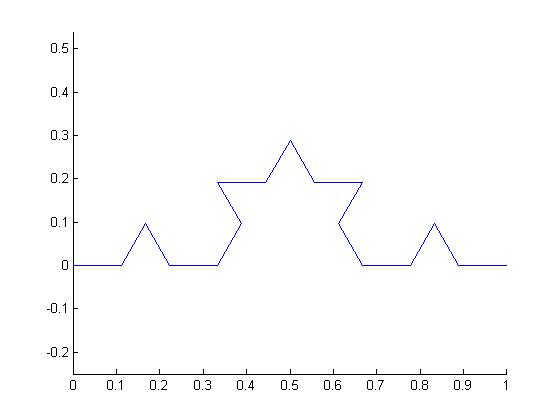
And this is how it looks after being applied twice...

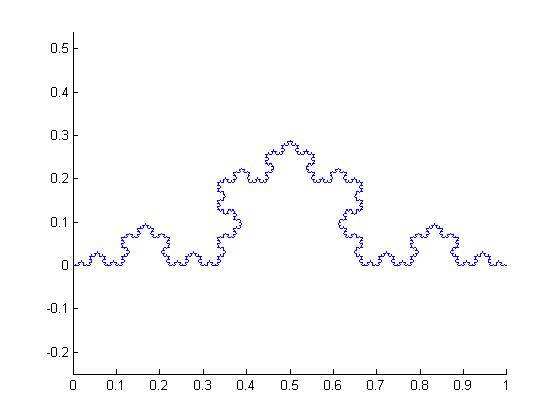
...or applied 7 times:

Finally, if you start with 3 sides (the triangle in figure 1), you'll get the Von Koch Snowflake.

---

Your task: Compute a von Koch Snowflake RECURSIVELY and display it. In the lab, Pauline will give help on the geometry. A useful geometric hint: the height of the spike is l/sqrt(12), i.e. if you would start with a line defined by the end points [0 0], [1 0], a single application of the construction rule would lead to line segments defined by the following 5 points: [0 0], [1/3 0], [0.5 1/sqrt(12)], [2/3 0], [1 0].

Recursion:

The stop case should test, if the line segment is shorter than a given threshold (e.g. shorter than 1). The length of a line segment with endpoints p1=(x1,y1) and p2=(x2,y2) is sqrt((x2-x1)^2+(y2-y1)^2). If the stop criterion is met, the segment’s endpoints should be stored in a list (Java LinkedList), followed by return().

This list will therefore contain all segments of the curve after the recursive computation has finished; it can then be displayed (custom graphics).

Your recursive function will therefore look like (pseudocode):

-----

function Koch(startpoint, endpoint)

if length(startpoint-endpoint)<1

store startpoint, endpoint in list

return

else

compute 5 points p1..p5 representing the updated segment

Koch(p1,p2)

Koch(p2,p3)

Koch(p3,p4)

Koch(p4,p5)

end

Good luck!